Einführung in die Digitale Elektronische Klangsynthese

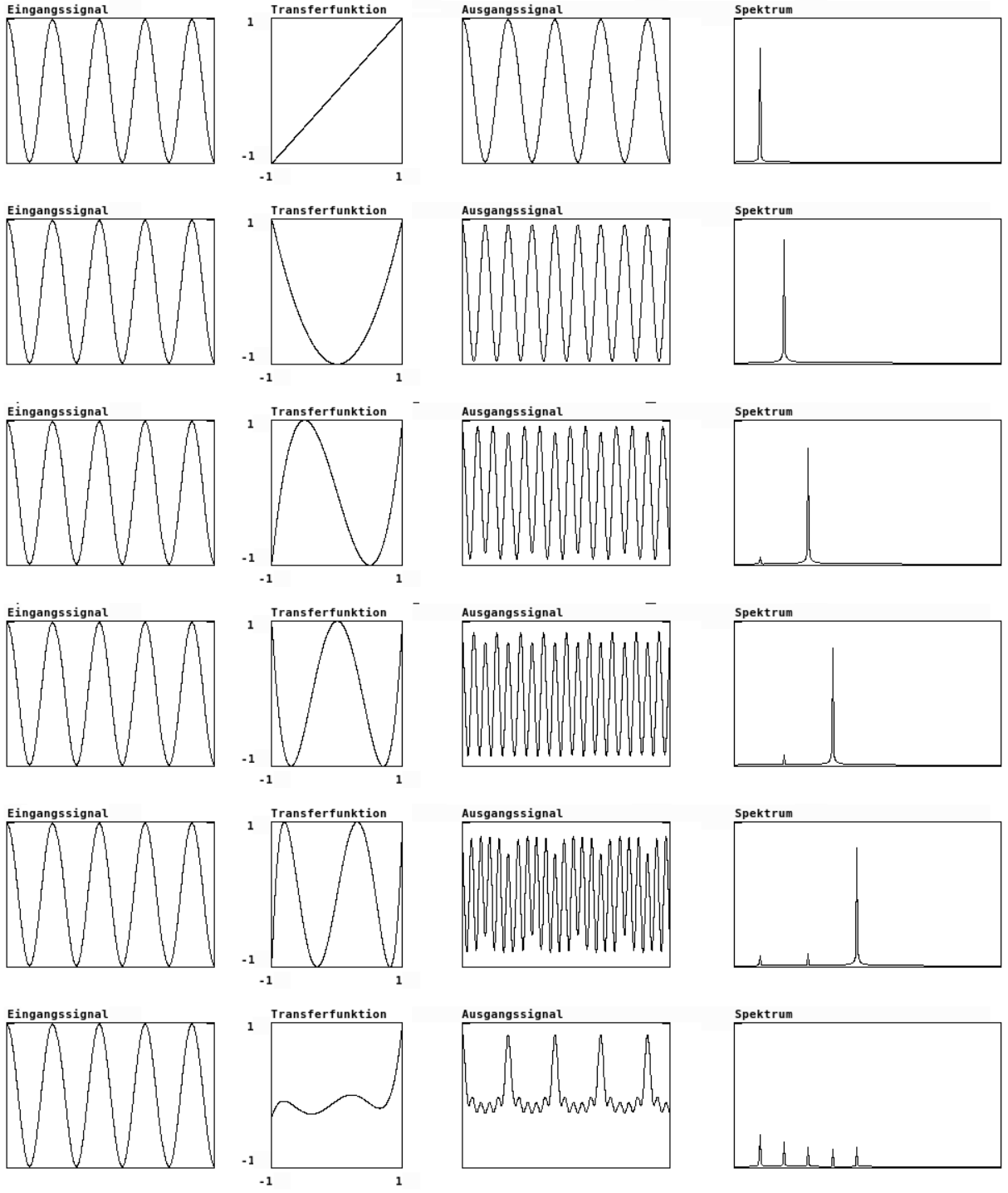
Chebyshev Polynome erster Art sind zum Koordinatenursprung punktsymmetrische bzw. zur y-Aches symmetrische Polynome, die vom Aussehen im Wertebereich [-1..1] trigonometrischen Funktionen ähneln. Dabei ist die Frequenz dieser "Sinusschwingungen" proportional zur Ordnung der Polynome (die 3. Ordnung entspricht dabei einer Sinusschwingung mit einer Periode im Wertebereich [-1..1]. Verwendet man diese Polynome als Transferfunktion, so wird bei hoher Eingangsamplitude der Partialton oberhalb des Eingangscosinussignals hervorgehoben, der der Ordnung des Chebyshov Polynoms entspricht. In Abb. 19 sind in den ersten fünf Zeilen die Chebyshev Polynome 1.-5. Ordnung als Transferfunktion verwendet worden (die Funktionen sind in der 2. Spalte (Transferfunktion) deutlich zu erkennen). Ein Vergleich der einzelnen Spektraldarstellungen zeigt deutlich, wie der Partialton, der dem Index der Chebyshev Funktion entspricht, hervortritt.

Die unterste Zeile zeigt das Ergebnis des Waveshaping mit einer Überlagerung der ersten fünf Chebyshev Polynome mit den relativen Amplituden 1, 0.685, 0.566, 0.456 und 0.535 als Transferfunktion.

Für eine andere künstlerische Verwendung von Waveshaping im Zusammenhang mit Chebyshev Polynomen siehe hier: http://cmc.music.columbia.edu/musicandcomputers/chapter4/04_06.php